



Version 1.1.1 built 2022-02-11 with R 4.1.2.
The library provides data sets (internal .rda and in CSV-format in /extdata/) supporting users in a black-box performance qualification (PQ) of their software installations. Users can analyze own data imported from CSV- and Excel-files. The methods given by the EMA for reference-scaling1,2 are implemented.
Potential influence of outliers on the variability of the reference can be assessed by box plots of studentized and standardized residuals as suggested at a joint EGA/EMA workshop.3
Health Canada’s approach4 requiring a mixed-effects model is approximated by intra-subject contrasts.
Direct widening of the acceptance range as recommended by the Gulf Cooperation Council5 (Bahrain, Kuwait, Oman, Qatar, Saudi Arabia, United Arab Emirates) is provided as well.
In full replicate designs the variability of test and reference treatments can be assessed by swT/swR and the upper confidence limit of σwT/σwR. This was required in a pilot phase by the WHO but lifted in 2021; reference-scaling of AUC is acceptable if the protocol is submitted to the PQT/MED.6
Called internally by functions method.A() and method.B(). A linear model of log-transformed pharmacokinetic (PK) responses and effects
sequence, subject(sequence), period
where all effects are fixed (i.e., ANOVA). Estimated by the function lm() of library stats.
modCVwR <- lm(log(PK) ~ sequence + subject%in%sequence + period,
data = data[data$treatment == "R", ])
modCVwT <- lm(log(PK) ~ sequence + subject%in%sequence + period,
data = data[data$treatment == "T", ])Called by function method.A(). A linear model of log-transformed PK responses and effects
sequence, subject(sequence), period, treatment
where all effects are fixed (e.g., by an ANOVA). Estimated by the function lm() of library stats.
Called by function method.B(). A linear model of log-transformed PK responses and effects
sequence, subject(sequence), period, treatment
where subject(sequence) is a random effect and all others are fixed.
Three options are provided:
lmer() of library lmerTest. method.B(..., option = 1) employs Satterthwaite’s approximation of the degrees of freedom equivalent to SAS’ DDFM=SATTERTHWAITE, Phoenix WinNonlin’s Degrees of Freedom Satterthwaite, and Stata’s dfm=Satterthwaite. Note that this is the only available approximation in SPSS.lme() of library nlme. method.B(..., option = 2) employs degrees of freedom equivalent to SAS’ DDFM=CONTAIN, Phoenix WinNonlin’s Degrees of Freedom Residual, STATISTICA’s GLM containment, and Stata’s dfm=anova. Implicitly preferred according to the EMA’s Q&A document and hence, the default of the function.lmer() of library lmerTest. method.B(..., option = 3) employs the Kenward-Roger approximation equivalent to Stata’s dfm=Kenward Roger (EIM) and SAS’ DDFM=KENWARDROGER(FIRSTORDER) i.e., based on the expected information matrix. Note that SAS with DDFM=KENWARDROGER and JMP calculate Satterthwaite’s [sic] degrees of freedom and apply the Kackar-Harville correction, i.e., based on the observed information matrix.Called by function ABE(). The model is identical to Method A. Conventional BE limits (80.00 – 125.00%) are employed by default. Tighter limits (90.00 – 111.11%) for narrow therapeutic index drugs (EMA and others) or wider limits (75.00 – 133.33%) for Cmax according to the guideline of South Africa7 can be specified.
TRTR | RTRT
TRRT | RTTR
TTRR | RRTT
TRTR | RTRT | TRRT | RTTR
TRRT | RTTR | TTRR | RRTT
TRT | RTR
TRR | RTT
TR | RT | TT | RR (Balaam’s design; not recommended due to poor power characteristics)
TRR | RTR | RRT
TRR | RTR (Extra-reference design; biased in the presence of period effects, not recommended)
Details about the reference datasets:
Results of the 30 reference datasets agree with ones obtained in SAS (9.4), Phoenix WinNonlin (6.4 – 8.1), STATISTICA (13), SPSS (22.0), Stata (15.0), and JMP (10.0.2).8
library(replicateBE) # attach the library
res <- method.A(verbose = TRUE, details = TRUE,
print = FALSE, data = rds01)
#
# Data set DS01: Method A by lm()
# -----------------------------------
# Type III Analysis of Variance Table
#
# Response: log(PK)
# Df Sum Sq Mean Sq F value Pr(>F)
# sequence 1 0.0077 0.007652 0.00268 0.9588496
# period 3 0.6984 0.232784 1.45494 0.2278285
# treatment 1 1.7681 1.768098 11.05095 0.0010405
# sequence:subject 75 214.1296 2.855061 17.84467 < 2.22e-16
# Residuals 217 34.7190 0.159995
#
# treatment T – R:
# Estimate Std. Error t value Pr(>|t|)
# 0.14547400 0.04650870 3.12788000 0.00200215
# 217 Degrees of Freedom
cols <- c(12, 17:21) # extract relevant columns
# cosmetics: 2 decimal places acc. to the GL
tmp <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp <- cbind(tmp, res[22:24]) # pass|fail
print(tmp, row.names = FALSE)
# CVwR(%) L(%) U(%) CL.lo(%) CL.hi(%) PE(%) CI GMR BE
# 46.96 71.23 140.40 107.11 124.89 115.66 pass pass passres <- method.B(option = 1, verbose = TRUE, details = TRUE,
print = FALSE, data = rds01)
#
# Data set DS01: Method B (option = 1) by lmer()
# ----------------------------------------------
# Response: log(PK)
# Type III Analysis of Variance Table with Satterthwaite's method
# Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
# sequence 0.001917 0.001917 1 74.7208 0.01198 0.9131536
# period 0.398078 0.132693 3 217.1188 0.82881 0.4792840
# treatment 1.579332 1.579332 1 216.9386 9.86464 0.0019197
#
# treatment T – R:
# Estimate Std. Error t value Pr(>|t|)
# 0.1460900 0.0465130 3.1408000 0.0019197
# 216.939 Degrees of Freedom (equivalent to SAS’ DDFM=SATTERTHWAITE)
cols <- c(12, 17:21)
tmp <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp <- cbind(tmp, res[22:24])
print(tmp, row.names = FALSE)
# CVwR(%) L(%) U(%) CL.lo(%) CL.hi(%) PE(%) CI GMR BE
# 46.96 71.23 140.40 107.17 124.97 115.73 pass pass passres <- method.B(option = 3, ola = TRUE, verbose = TRUE,
details = TRUE, print = FALSE, data = rds01)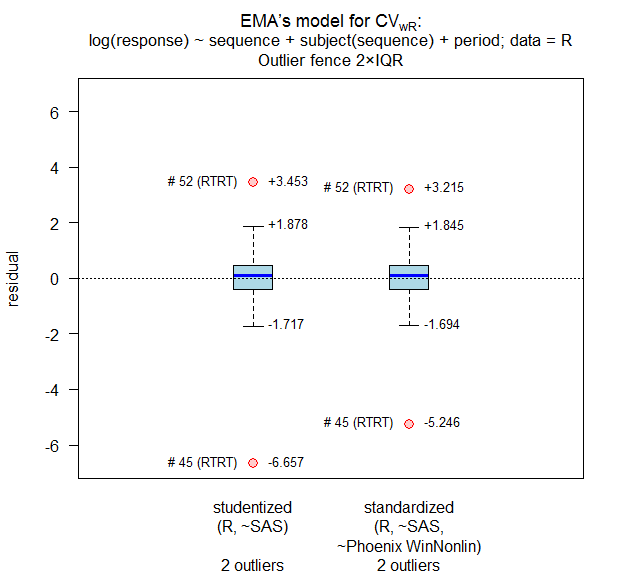
#
# Outlier analysis
# (externally) studentized residuals
# Limits (2×IQR whiskers): -1.717435, 1.877877
# Outliers:
# subject sequence stud.res
# 45 RTRT -6.656940
# 52 RTRT 3.453122
#
# standarized (internally studentized) residuals
# Limits (2×IQR whiskers): -1.69433, 1.845333
# Outliers:
# subject sequence stand.res
# 45 RTRT -5.246293
# 52 RTRT 3.214663
#
# Data set DS01: Method B (option = 3) by lmer()
# ----------------------------------------------
# Response: log(PK)
# Type III Analysis of Variance Table with Kenward-Roger's method
# Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
# sequence 0.001917 0.001917 1 74.9899 0.01198 0.9131528
# period 0.398065 0.132688 3 217.3875 0.82878 0.4792976
# treatment 1.579280 1.579280 1 217.2079 9.86432 0.0019197
#
# treatment T – R:
# Estimate Std. Error t value Pr(>|t|)
# 0.1460900 0.0465140 3.1408000 0.0019197
# 217.208 Degrees of Freedom (equivalent to Stata’s dfm=Kenward Roger EIM)
cols <- c(27, 31:32, 19:21)
tmp <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp <- cbind(tmp, res[22:24])
print(tmp, row.names = FALSE)
# CVwR.rec(%) L.rec(%) U.rec(%) CL.lo(%) CL.hi(%) PE(%) CI GMR BE
# 32.16 78.79 126.93 107.17 124.97 115.73 pass pass passres <- method.A(regulator = "GCC", details = TRUE,
print = FALSE, data = rds01)
cols <- c(12, 17:21)
tmp <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp <- cbind(tmp, res[22:24])
print(tmp, row.names = FALSE)
# CVwR(%) L(%) U(%) CL.lo(%) CL.hi(%) PE(%) CI GMR BE
# 46.96 75.00 133.33 107.11 124.89 115.66 pass pass passres <- ABE(theta1 = 0.75, details = TRUE,
print = FALSE, data = rds01)
tmp <- data.frame(as.list(sprintf("%.2f", res[12:17])))
names(tmp) <- names(res)[12:17]
tmp <- cbind(tmp, res[18])
print(tmp, row.names = FALSE)
# CVwR(%) BE.lo(%) BE.hi(%) CL.lo(%) CL.hi(%) PE(%) BE
# 46.96 75.00 133.33 107.11 124.89 115.66 passres <- ABE(theta1 = 0.90, details = TRUE,
print = FALSE, data = rds05)
cols <- c(13:17)
tmp <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp <- cbind(tmp, res[18])
print(tmp, row.names = FALSE)
# BE.lo(%) BE.hi(%) CL.lo(%) CL.hi(%) PE(%) BE
# 90.00 111.11 103.82 112.04 107.85 failThe package requires R ≥3.5.0. However, for the Kenward-Roger approximation method.B(..., option = 3) R ≥3.6.0 is required.
To use the development version, please install the released version from CRAN first to get its dependencies right (readxl ≥1.0.0, PowerTOST ≥1.5.3, lmerTest, nlme, pbkrtest).
You need tools for building R packages from sources on your machine. For Windows users:
devtools and build the development version by:install.packages("devtools", repos = "https://cloud.r-project.org/")
devtools::install_github("Helmut01/replicateBE")Inspect this information for reproducibility. Of particular importance are the versions of R and the packages used to create this workflow. It is considered good practice to record this information with every analysis.
sessionInfo()
# R version 4.1.2 (2021-11-01)
# Platform: x86_64-w64-mingw32/x64 (64-bit)
# Running under: Windows 7 x64 (build 7601) Service Pack 1
#
# Matrix products: default
#
# locale:
# [1] LC_COLLATE=German_Germany.1252 LC_CTYPE=German_Germany.1252
# [3] LC_MONETARY=German_Germany.1252 LC_NUMERIC=C
# [5] LC_TIME=German_Germany.1252
#
# attached base packages:
# [1] stats graphics grDevices utils datasets methods base
#
# other attached packages:
# [1] replicateBE_1.1.1
#
# loaded via a namespace (and not attached):
# [1] tidyselect_1.1.1 xfun_0.29 purrr_0.3.4
# [4] splines_4.1.2 lmerTest_3.1-3 lattice_0.20-45
# [7] colorspace_2.0-2 vctrs_0.3.8 generics_0.1.2
# [10] htmltools_0.5.2 yaml_2.2.2 utf8_1.2.2
# [13] rlang_1.0.1 pillar_1.7.0 nloptr_2.0.0
# [16] glue_1.6.1 PowerTOST_1.5.3.9000 readxl_1.3.1
# [19] lifecycle_1.0.1 stringr_1.4.0 munsell_0.5.0
# [22] gtable_0.3.0 cellranger_1.1.0 mvtnorm_1.1-3
# [25] evaluate_0.14 knitr_1.37 fastmap_1.1.0
# [28] parallel_4.1.2 pbkrtest_0.5.1 fansi_1.0.2
# [31] highr_0.9 broom_0.7.12 Rcpp_1.0.8
# [34] backports_1.4.1 scales_1.1.1 lme4_1.1-28
# [37] TeachingDemos_2.12 ggplot2_3.3.5 digest_0.6.29
# [40] stringi_1.7.6 dplyr_1.0.7 numDeriv_2016.8-1.1
# [43] grid_4.1.2 cli_3.1.1 tools_4.1.2
# [46] magrittr_2.0.2 tibble_3.1.6 tidyr_1.2.0
# [49] crayon_1.4.2 pkgconfig_2.0.3 MASS_7.3-55
# [52] ellipsis_0.3.2 Matrix_1.4-0 minqa_1.2.4
# [55] rmarkdown_2.11 rstudioapi_0.13 cubature_2.0.4.2
# [58] R6_2.5.1 boot_1.3-28 nlme_3.1-155
# [61] compiler_4.1.2Helmut Schütz (author) ORCID iD
Michael Tomashevskiy (contributor)
Detlew Labes (contributor) ORCID iD
Package offered for Use without any Guarantees and Absolutely No Warranty. No Liability is accepted for any Loss and Risk to Public Health Resulting from Use of this R-Code.
1. European Medicines Agency. EMA/582648/2016. Annex I. 21 September 2016. ↩︎
2. European Medicines Agency. Committee for Medicinal Products for Human Use. CPMP/EWP/QWP/1401/98 Rev. 1/ Corr **. 20 January 2010. ↩︎
3. European Generic Medicines Association. Revised EMA Bioequivalence Guideline. Questions & Answers. London, June 2010. ↩︎
4. Health Canada. Guidance Document. Conduct and Analysis of Comparative Bioavailability Studies. 2018/06/08. ↩︎
5. Executive Board of the Health Ministers’ Council for GCC States. The GCC Guidelines for Bioequivalence. Version 3.0. May 2021. ↩︎
6. World Health Organization. Application of reference-scaled criteria for AUC in bioequivalence studies conducted for submission to PQT/MED. 02 July 2021. ↩︎
7. Medicines Control Council. Registration of Medicines. Biostudies. June 2015. ↩︎
8. Schütz H, Tomashevskiy M, Labes D, Shitova A, González-de la Parra M, Fuglsang A. Reference Datasets for Studies in a Replicate Design Intended for Average Bioequivalence with Expanding Limits. AAPS J. 2020; 22(2): Article 44. doi:10.1208/s12248-020-0427-6. ↩︎
9. European Medices Agency. EMA/582648/2016. Annex II. 21 September 2016. ↩︎
10. Shumaker RC, Metzler CM. The Phenytoin Trial is a Case Study of ‘Individual’ Bioequivalence. Drug Inf J. 1998; 32(4): 1063–1072. doi:10.1177/009286159803200426. ↩︎